EJEMPLOS DESARROLLADOS

A continuación, vamos a presentar algunos ejemplos de ecuaciones exponenciales desarrollados. También, en cada ejercicio colocamos el link para que puedas acceder y encontrar mas ejemplos.

Ejemplo 1 

Resolver mediante el cambio de variable $t=3^x$:

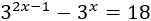
solución 

Escribimos la exponencial $3^{2x-1}$ como una potencia de 3 por una exponencial al cuadrado y aplicamos el cambio de variable $t=3^x$:

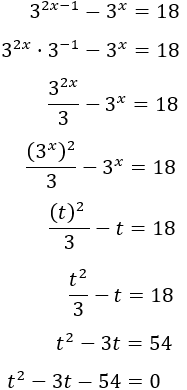
Las soluciones de la ecuación de segundo grado son

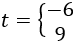
Como $t=3^x$, tenemos

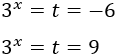
La primera ecuación, $3^x=-6$ no tiene solución real. De la segunda ecuación tenemos que $x=2$

• https://www.problemasyecuaciones.com/Ecuaciones/exponenciales/ecuaciones-exponenciales-resueltas-ejemplos-explicadas-soluciones-raices-exponentes.html

Ejemplo 2

Aplicamos las propiedades de las potencias del producto o el cociente, para quitar las sumas o restas de los exponentes

Realizamos el cambio de variable

Quitamos denominadores

Resolvemos la ecuación y deshacemos el cambio de variable

No tiene solución porque una potencia con base positiva no puede dar un número negativo

• https://www.superprof.es/apuntes/escolar/matematicas/algebra/log/ecuacion-exponencial-12.html.

Ejemplo 3

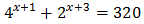
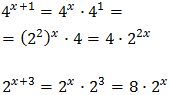
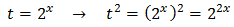
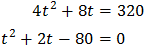
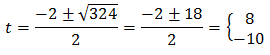
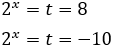
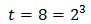
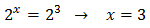
Halla el conjunto solución de la ecuación:

.

Solución:

• Para expresar ambos miembros de la ecuación como potencias de la misma base a simple vista puedes deducir que debes llevar la ecuación a base 3
   (En el miembro izquierdo debes aplicar la propiedad producto de potencias de igual base en el miembro derecho, la propiedad de potencia de exponente negativo)
   (Reduces los términos semejantes)
• Igualas los exponentes y resuelves la ecuación lineal obtenida .
  
   (Transpones el 1)
   (Reduces términos semejantes)
   (Despejas la variable)
   (Efectúas el cociente)
• Compruebas y escribes la solución.
  

NOTA: Como en esta ecuación solamente se han aplicado transformaciones equivalentes no resulta obligatoria la comprobación.

• http://matematica.cubaeduca.cu/media/matematica.cubaeduca.cu/medias/interactividades/piu/25ecuac_expon/co/Ecuaciones_exponenciales_3.html.

Ejemplo 4

Las bases de las exponenciales son distintas, pero ambas son potencias de 2. Operamos para tener potencias con la misma base:

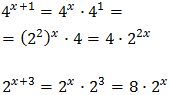
Con lo que podemos reescribir la ecuación como

Aplicamos un cambio de variable:

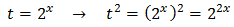
Substituimos en la ecuación y obtenemos la ecuación de segundo grado

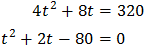
cuyas soluciones son

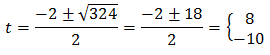
Por tanto,

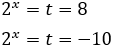
La segunda solución no es posible por ser negtiva. Por tanto,

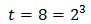
Es decir, debe cumplirse

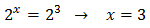
La única solución de la ecuación exponencial es x = 3.

• http://procomun.educalab.es/es/articulos/ecuaciones-exponenciales