- RODRIGUEZ GUEVARA, DANY
- QUISPE ROJAS, CARLOS
- FLORES HERNANDEZ, NEBERLY
- CEBREROS GARCIA, CHRISTIAN
En este blog te mostraremos y ayudaremos a entender y desarrollar el tema "ECUACIONES EXPONENCIALES". de una forma práctica y sencilla con ejemplos diversos y te llevaremos a diferentes paginas con respecto al tema para que puedas tener una visión amplia del tema.
sábado, 27 de abril de 2019
INTEGRANTES
viernes, 26 de abril de 2019
PRESENTACIÓN
En el siguiente blog te mostraremos y ayudaremos a entender el tema "ECUACIONES EXPONENCIALES", de una forma práctica y sencilla. Para ello, te mostraremos diversos ejemplos y también colocaremos diferentes enlaces de paginas para que de esa manera te puedan ayudar a complementar y tener una visión mas amplia del tema en cuestión.
jueves, 25 de abril de 2019
OBETIVO DEL BLOG
El objetivo de este blog, es que a través de ello podamos aprender de una manera mas eficaz y sencilla, sobre las ecuaciones exponenciales. Aplicando las propiedades que estamos facilitando, seguido de los ejemplos resueltos. Con el fin de compartir y transformar el conocimiento del tema que estamos brindando.
miércoles, 24 de abril de 2019
INTRODUCCIÓN
-
Las funciones exponenciales tienen aplicaciones en todos los campos del quehacer humano. Son particularmente útiles en el estudio de la química, la física, la biología y la ingeniería para describir la forma en que varían las cantidades.
- En la vida cotidiana hay diferentes fenómenos cuyo desarrollo tiene forma exponencial. Para el análisis de su comportamiento es necesario realizar cálculos donde se utilizan las potencias.
- Es por ello que tiene gran importancia el saber realizar cálculos con potencias y resolver ecuaciones exponenciales.
- Las ecuaciones exponenciales, al igual que las ecuaciones con radicales se encuentran entre las ecuaciones irracionales.
martes, 23 de abril de 2019
DEFINICIÓN
Se llama función exponencial de base a, a aquella cuya forma genérica es f (x)
= ax
, siendo a un número positivo distinto de 1.
Por lo tanto, en una función exponencial la variable independiente (abscisa) es
el exponente de la función.
Por su propia definición, el dominio de toda función exponencial es el conjunto
de los números reales R.
Función exponencial según el valor de la base.
Si 0 < a < 1, entonces f(x) = ax es decreciente, puesto que la base es una fracción positiva o decimal menor que 1. Luego si el exponente aumenta, entonces el valor de ax disminuye.
Si a > 1 entonces f(x) = ax es creciente, puesto que la base es un número positivo mayor que 1. Luego, si el exponente aumenta, entonces el valor de ax también aumenta.
La base no puede ser igual a 0 porque cualquier número exponencial de base cero es igual a 1, resultando la función y = 1x , la cual no tendría sentido, debido a que su valor es constantemente igual a 1, con lo que gráficamente es una función constante y = 1 (recta paralela al eje X en el punto y = 1).
La base no puede ser negativa porque el valor de la función será positivo si x es par y negativo si el exponente es impar. Además, si x es una fracción como ½, entonces la función no tiene imagen en los reales.
Referencia bibliográfica
http://ww2.educarchile.cl/UserFiles/P0001/File/exponenciales_%20logaritmos.pdf
Función exponencial según el valor de la base.
Si 0 < a < 1, entonces f(x) = ax es decreciente, puesto que la base es una fracción positiva o decimal menor que 1. Luego si el exponente aumenta, entonces el valor de ax disminuye.
Si a > 1 entonces f(x) = ax es creciente, puesto que la base es un número positivo mayor que 1. Luego, si el exponente aumenta, entonces el valor de ax también aumenta.
La base no puede ser igual a 0 porque cualquier número exponencial de base cero es igual a 1, resultando la función y = 1x , la cual no tendría sentido, debido a que su valor es constantemente igual a 1, con lo que gráficamente es una función constante y = 1 (recta paralela al eje X en el punto y = 1).
La base no puede ser negativa porque el valor de la función será positivo si x es par y negativo si el exponente es impar. Además, si x es una fracción como ½, entonces la función no tiene imagen en los reales.
Referencia bibliográfica
http://ww2.educarchile.cl/UserFiles/P0001/File/exponenciales_%20logaritmos.pdf
lunes, 22 de abril de 2019
PROPIEDADES DE UNA ECUACIÓN EXPONENCIAL
¿Cuáles son las propiedades de las potencias?
Referencia bibliográfica
domingo, 21 de abril de 2019
VIDEOS EXPLICATIVOS
En este lugar encontraras vídeos relacionado al tema principal con lo cual queremos ayudarte a entender claramente todo lo que necesitas saber para poder resolver fácilmente un ejercicio de este.
CHRISTIAN (Archivo del video)
DANY (Archivo del video)
NEBERLY (Archivo del video)
CARLOS (Archivo del vídeo)
sábado, 20 de abril de 2019
EJEMPLOS DESARROLLADOS
A continuación, vamos a presentar algunos ejemplos de ecuaciones exponenciales desarrollados. También, en cada ejercicio colocamos el link para que puedas acceder y encontrar mas ejemplos.
Ejemplo 1
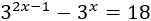
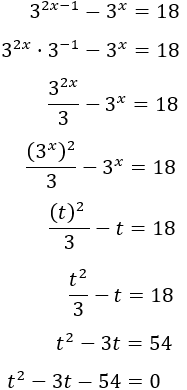
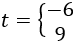
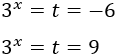






Ejemplo 1
Resolver mediante el cambio de variable t=3x:
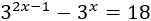
solución
Escribimos la exponencial 32x−1 como una potencia de 3 por una exponencial al cuadrado y aplicamos el cambio de variable t=3x:
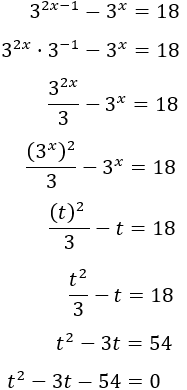
Las soluciones de la ecuación de segundo grado son
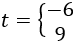
Como t=3x, tenemos
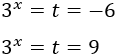
La primera ecuación, 3x=−6 no tiene solución real. De la segunda ecuación tenemos que x=2
Ejemplo 2

Aplicamos las propiedades de las potencias del producto o el cociente, para quitar las sumas o restas de los exponentes

Realizamos el cambio de variable


Quitamos denominadores

Resolvemos la ecuación y deshacemos el cambio de variable

No tiene solución porque una potencia con base positiva no puede dar un número negativo
Ejemplo 3
 .
.
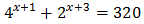
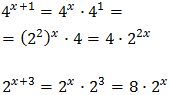

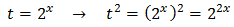
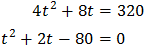
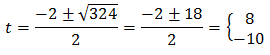
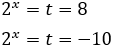
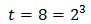
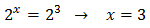
Halla el conjunto solución de la ecuación:
Solución:
- Para expresar ambos miembros de la ecuación como potencias de la misma base a simple vista puedes deducir que debes llevar la ecuación a base 3
(En el miembro izquierdo debes aplicar la propiedad producto de potencias de igual base en el miembro derecho, la propiedad de potencia de exponente negativo)
(Reduces los términos semejantes)
- Igualas los exponentes y resuelves la ecuación lineal obtenida .
(Transpones el 1)
(Reduces términos semejantes)
(Despejas la variable)
(Efectúas el cociente)
- Compruebas y escribes la solución.
NOTA: Como en esta ecuación solamente se han aplicado transformaciones equivalentes no resulta obligatoria la comprobación.
Ejemplo 4
Las bases de las exponenciales son distintas, pero ambas son potencias de 2. Operamos para tener potencias con la misma base:
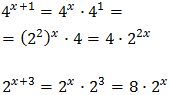
Con lo que podemos reescribir la ecuación como

Aplicamos un cambio de variable:
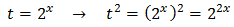
Substituimos en la ecuación y obtenemos la ecuación de segundo grado
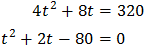
cuyas soluciones son
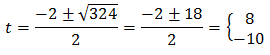
Por tanto,
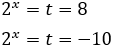
La segunda solución no es posible por ser negtiva. Por tanto,
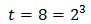
Es decir, debe cumplirse
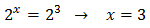
La única solución de la ecuación exponencial es x = 3.
viernes, 19 de abril de 2019
VIDEOS RELACIONADOS AL TEMA
A continuación presentamos algunos vídeos explicativos relacionados con nuestro tema ECUACIONES EXPONENCIALES. Esperemos que le sean de gran ayuda.
jueves, 18 de abril de 2019
CONCLUSIÓN
En definitiva, el principal motivo de este blog es simplificar y hacer práctica la comprensión del tema abordado "Ecuaciones Exponenciales", y que todos los que visiten está pagina puedan entender y desarrollar ejercicios de primer y segundo grado.
miércoles, 17 de abril de 2019
PAGINAS RELACIONADAS AL TEMA
- http://ww2.educarchile.cl/UserFiles/P0001/File/exponenciales_%20logaritmos.pdf.
- https://www.problemasyecuaciones.com/Ecuaciones/exponenciales/ecuaciones-exponenciales-resueltas-ejemplos-explicadas-soluciones-raices-exponentes.html.
- https://www.superprof.es/apuntes/escolar/matematicas/algebra/log/ecuacion-exponencial-12.html.
- http://matematica.cubaeduca.cu/media/matematica.cubaeduca.cu/medias/interactividades/piu/25ecuac_expon/co/Ecuaciones_exponenciales_3.html.
- http://procomun.educalab.es/es/articulos/ecuaciones-exponenciales
Suscribirse a:
Comentarios (Atom)






